Paper 解讀 - 打造公平的遊戲轉蛋:在不洩漏原始碼的前提下驗證虛擬轉蛋的機率
這篇是 HITCON CMT 2023 的演講 今天就來解讀一下這篇在講什麼。我在現場聽的時候,被突如其來的數學打得頭昏眼花,事後看懂才寫了這篇 xD
背景
丁特事件中,遊戲橘子公告的機率與實際上抽的機率不符合,但消費者又無法驗證,所以作者就想知道能不能設計出一個,可以在不開源的情況下驗證官方公告的機率是否為真的系統。以下是幾個重要事件的時間線。
- 2021/06 → 轉蛋法聯署
- 2021/08 → 丁特事件
- 2023/01 → 轉蛋法生效,參考日本、韓國的轉蛋法
值得注意的是日本有限制保底抽數、金額。 而大家在意的是怎麼驗證機率。
Related Works
這邊提到了兩篇 related works,但有一些各自的問題
- gacha.gamelab.com.tw
- 第三方驗證平台(壞掉了?),玩家自行上傳抽獎紀錄
- (PDF) Bringing transparency and trustworthiness to loot boxes with blockchain and smart contracts (researchgate.net)
- 嘗試用 smart contract 來解決這個問題,但是這樣就是 open source 了
- 而且在 smart contract 上還有 random source 的問題
怎麼做
轉蛋主要由兩個部分組成,隨機來源 + 轉蛋函式。 所以要可以驗證轉蛋的機率代表我們需要,可以驗證的隨機來源 + 可以驗證的轉蛋函式
Verifiable Random Source
簡單作法
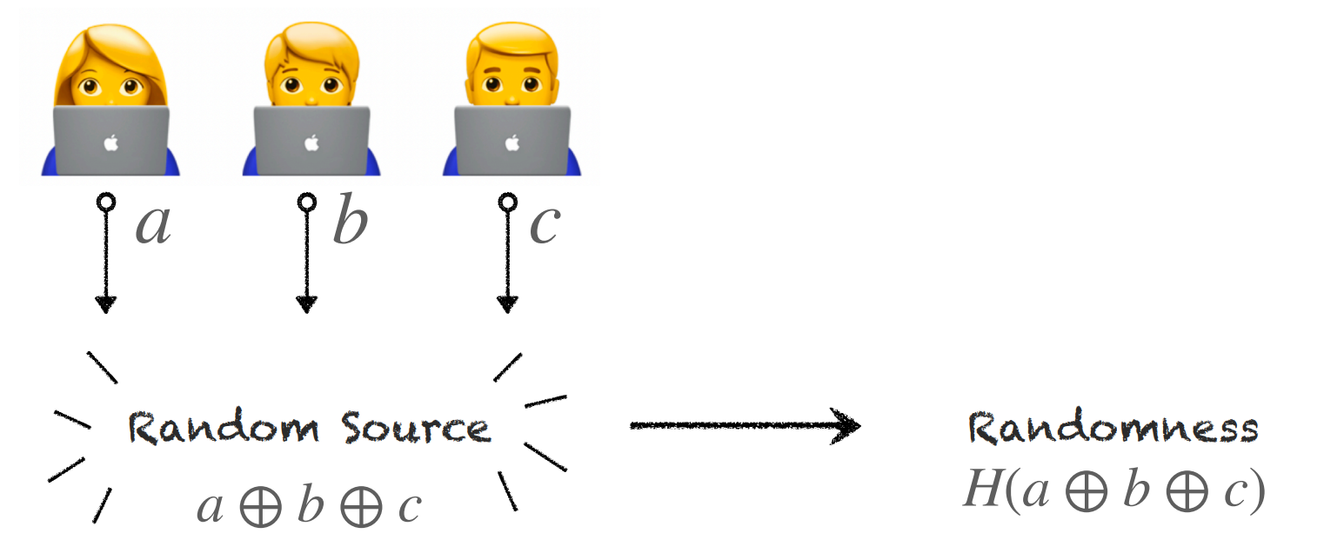
所有人提供一個 random number,把大家的 xor 起來 但是這樣做可能會有 Last Contribution Attack,也就是最後一個人 C 可以暴力的嘗試不同的 c 值,選一個可以中獎的,等於最後一個人可以操控結果
HeadStart
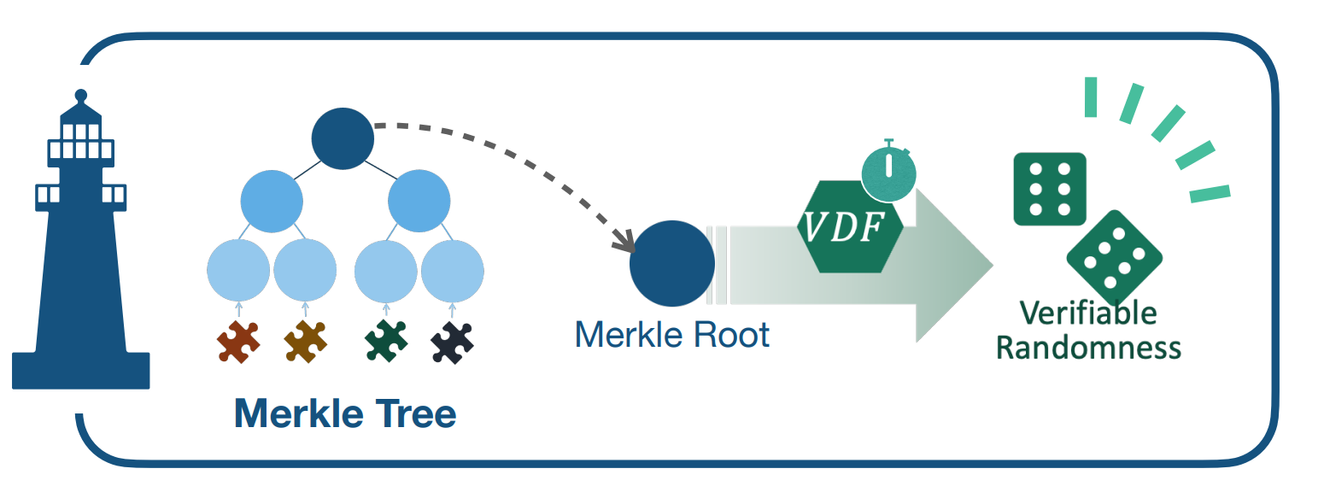
所以這邊他們改良了前面的作法,這個作法叫做 HeadStart,這也是作者同一個實驗室他們發的論文。 這個作法主要改動了兩個部分
- 把大家的 random number 做成 Merkle Tree
- 最後會經過 Verifiable Delay Function (VDF) 的運算得到最後結果
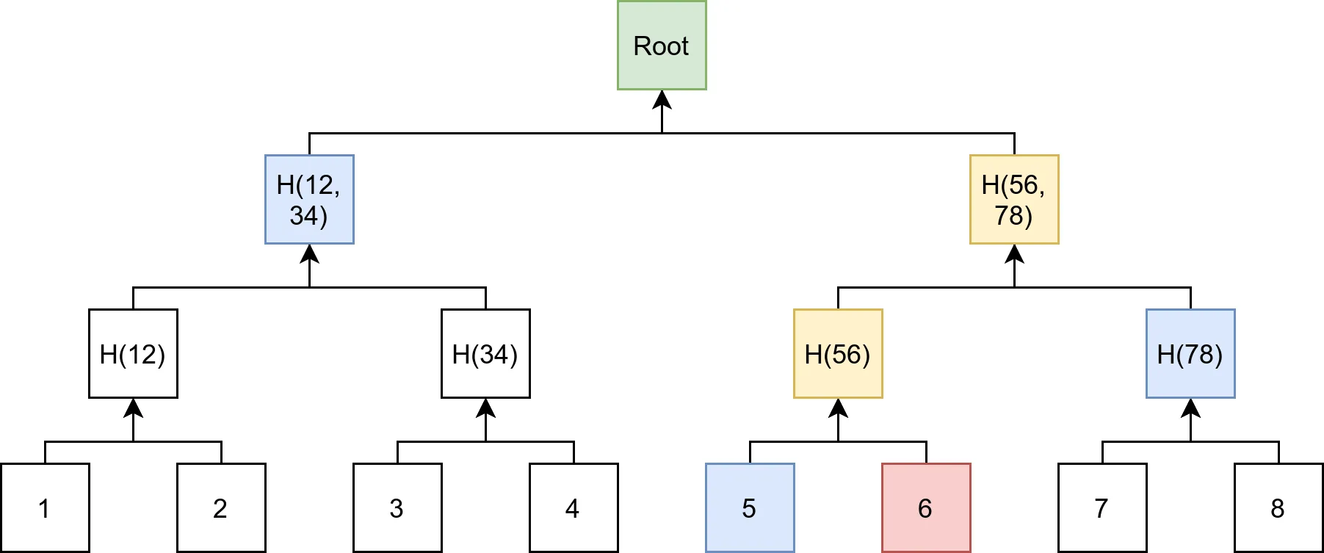
做成 Merkle Tree 的主要好處是,驗證只需要 O(logN) 的時間和空間
VDF 則是一個需要一定的時間計算,但是可以被迅速驗證 (有點像是 Blockchain 的 POC,但是 VDF 不能被 parallelized),因為計算需要一定的時間,所以就可以避免 Last Contribution Attack
Verifiable Function
接著有了 Verifiable Random Source 之後,我們還需要 Verifiable Function。 這邊作者直接採用了一種 Zero Knowledge Proof 叫做 PLONK。原本我們的函式長這樣 f(x) = y,那加上這個 PLONK 之後,他就會多吐出一個 proof 讓我們驗證,f(x) = y + proof。這邊其實不需要理解數學的細節,總之可以在不公開函式的情況下驗證你是用同一個函式去算出 x 的結果 y,而不是我給你輸入你才又偷偷換了另一個每次都抽不到的函式。如果真的想了解的同學可以看一下 Vitalik 大神的 ZKP 系列。
實際的流程
前面介紹了必要的元件之後,我們就可以來看實際的抽卡流程是怎麼個樣子
Probability Verification Protocol
今天我想測一下這個遊戲的機率是不是唬爛的,我就可以發起這個驗證的流程 (沒有真的抽卡,只是模擬抽卡)。 可以想像函式 f 就是一個下面這樣的函式,吃兩個參數,random source r 和遊戲參數 o。 遊戲參數裡面會有像是 VIP 等級、抽卡次數等,比如抽卡次數就很有用,可以根據抽獎次數計算要不要保底。
def loot(seed, params):
random.seed(seed)
num = random.randint(0, 999)
# 20 抽保底
if params["抽獎次數"] >= 19:
return 1
# 機率 10%
if num < 100:
return 1
else:
return 0
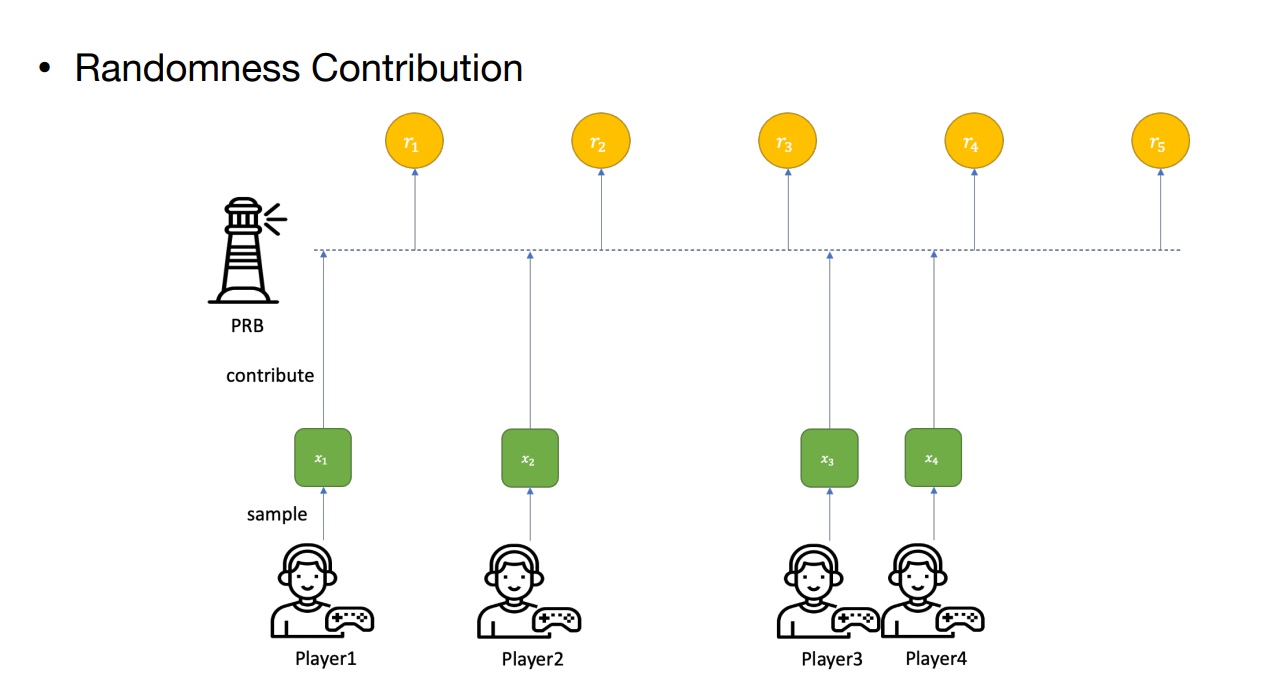
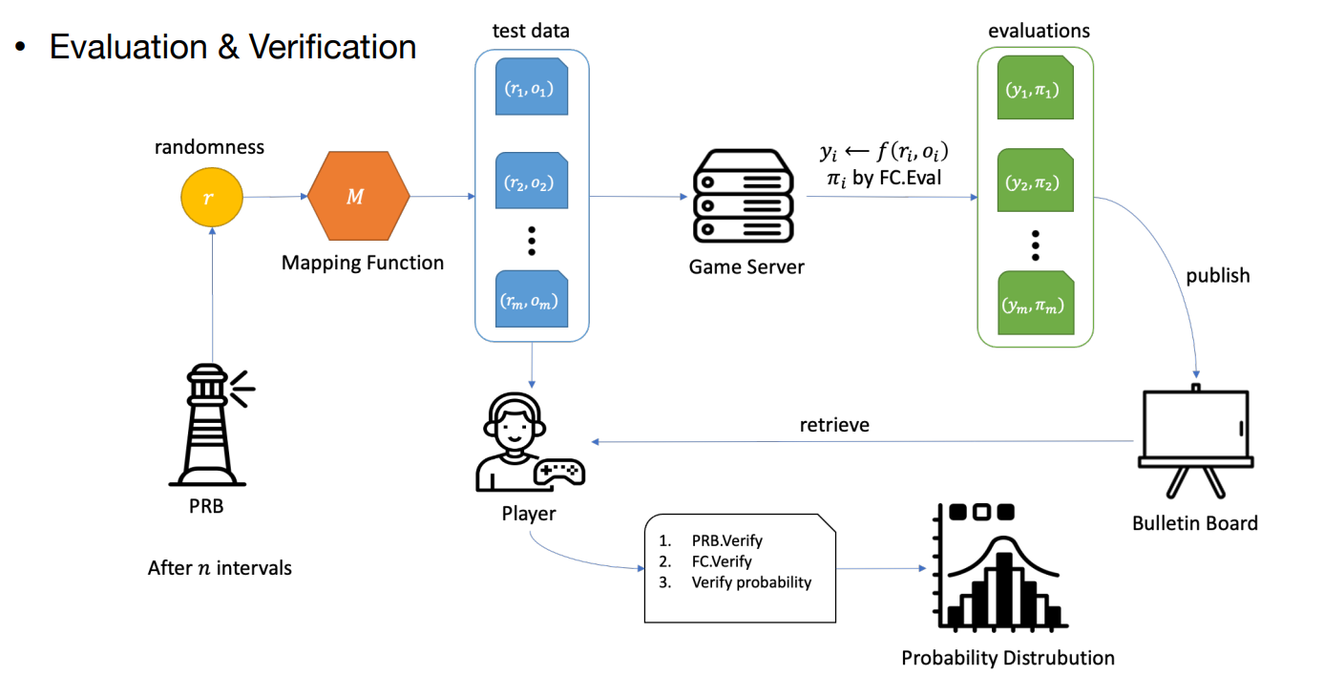
- 首先,會有一個 Random Beacon 收集大家貢獻的 randomness,收集滿了之後,吐出 100 個 test data (模擬 100 次抽卡)
- 假設是 m = 100 的話 (方便想像)
- 這些 test data 就會丟進去函式裡面運算,最後吐出 100 個 (抽卡結果, 證明),這些都會放在公告欄裡面
- 最後,玩家們就可以拿 test data 和公佈欄裡面的 (抽卡結果, 證明) 去驗證函式 (透過 PLONK 的 ZKP 證明)
- 驗證正確代表函式沒有被動手腳,所以就可以直接來算算看這 100 個抽卡結果的中獎機率是多少啦
- 論文中還有計算說,如果官方說是 0.3 的機率,哪麼驗證出來的機率要小於多少就有很高機率他在說謊
Loot Box Opening Protocol
最後是真的要抽卡的時候的流程 (作者畫的圖好複雜,不貼了 xD)
- Setup
- (Server) 先算出一個 Hash Chain,然後把
a_n給玩家a_i = H(a_i-1)a_0 -> a_1 -> a_2 -> ... -> a_n
- (Server) 先算出一個 Hash Chain,然後把
- 以下步驟可以重複多次
- Evaluation (開抽)
- (Player) 隨機選一個 random 數
B,還有一些遊戲參數O(比如 VIP 等級、抽獎次數等),傳給 Server - (Server) 上次 Hash Chain 選到
a_i,這次就挑a_i-1。 計算 random source 等於a_i-1 || B(合併雙方的 random source),帶入抽卡函式f(a_i-1 || B, O) = y + proof。最後把結果(y, proof, a_i-1)傳回去給玩家
- (Player) 隨機選一個 random 數
- Verification
- (Player) 拿到 proof 可以驗證是同一個函式
- (Player) 拿到
a_i-1可以驗證H(a_i-1) = a_i(代表 Server 不是隨心所欲的亂選一個隨機數而是在玩家選出B之前就已經決定好a_i-1了)
- Evaluation (開抽)
這邊的重點其實是 Hash Chain 的部分,可以確保 Server 不是在收到玩家選的 random source B 之後,才挑一個抽不到卡的 random source。
結論
就是因為不想開源,所以才需要 ZKP,但仔細思考一下,其實 ZKP 的部分跟其他 Protocol 可以完全切開,ZKP 在這裡扮演的就是確保遊戲廠商至始至終都是用同一個函式,不會在模擬抽卡和真正抽卡的時候用不同的函式,這樣就可以用模擬抽卡來驗證機率了。把 ZKP 的部分去掉之後看,就會發現其實沒這麼複雜 xD (不要上來就貼數學式 RRR)
再來的問題就只是 Random Source 怎麼來
- 模擬抽卡: 用 HeadStart 讓大家貢獻 Random Source
- 真的開抽: Server 和 Player 雙方各貢獻一個 Random Source,然後 Server 用 Hash Chain 來證明他在 Player 選 Random Source 之前就已經選好了,不是拿到 Player 的 Random Source 才挑的
要開源的話,其實只要抽卡部分的程式碼可以開源就好了吧,這樣就完全不用 ZKP,實作就只剩 Hash Chain 那邊要實作,其他通通不需要了,模擬抽卡什麼的也不用了,都已經有 source code 看就知道機率是多少,要驗證函式的話,你只要把輸入丟進去看輸出是不是一樣的就好。
References
- 他們的簡報: 打造公平的遊戲轉蛋_在不洩漏原始碼的前提下驗證虛擬轉蛋的機率.pdf
- 他們的論文: ntu-111-2.pdf
- 他們的原始碼: WangJ509/LootBoxVerification (github.com)
載入評論區...